Quadratic Sieve and others

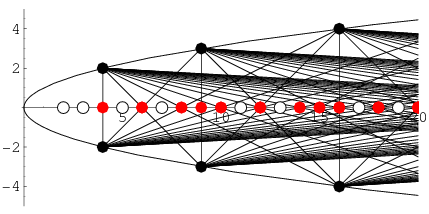
Was procrastinating grading my exams and wandering along on wolfram Mathworld's website when I came across this sweet diagram, and a concept I had never heard of...

Start by drawing the basic parabola curve (y=x²).  Above you'll see the curve, although it's rotated to show along the x-axis instead.  Now find all the pretty points, that is, the places where the curve has nice integer coordinates, such as (1,1), (2, 4), (3, 9), (4, 16), etc, as well as (-4, 16) and so on.  If you connect all the "pretty points" with line segments, ignoring (0,0), (1,1), and (-1, 1), the line segments will all intersect the axis at "pretty" intercepts -- that is at nice integers, never at fractions or decimal locations.  Now that alone is cool...

... but if you notice from the picture, they don't intersect at ALL the pretty points.  They only intersect at specific locations, 4, 6, 8, 9, 10, 12, 14.  What's most interesting is the points that AREN'T crossed, 2, 3, 5, 7, 11, 13....  The prime numbers!  How cool is it, that if we continued this drawing forever, we would cross out all the composite numbers and leave behind all the primes.  This sifting of the numbers is why this particular scheme is called the Quadratic Sieve.

You might recall from algebra class hearing about the Sieve of Eratosthenes?  It works by going and counting by 2's and crossing every number, then counting by 3's and crossing out every number, and then 5's, and 7's, etc, until all that's left not crossed is the prime numbers.

Standard Form Fight Song

Standard form usually get's a bad rep, perhaps because slope-intercept (or y=mx+b) form is so popular due to its ease in graphing. Standard form, while not as easy to graph, does have its benefits, a few of which I'll list below.

As a recap, standard form is writing an equation as Ax+By = C, with the stipulation that A, B, and C must be integers.  I prefer the form Ax-By=C instead of + because then the A and the B values end up being the rise and the run of the line.  For example, 2x-5y=20 has a rise of 2 units for every run of 5 units, for a slope of 2/5.  Additionally, the example x+3y=15 rises 1 unit for every run of 3 units backward -- backwards because it was written with + instead of -.

Here's some reasons I think standard form is useful:

• It's neat and orderly, with no fractions or decimals
• It's easy to plug in points (because x and y are in order and the multipliers are always integers) which is how you check if a point is on a line
• It still reveals rise and run, with some understanding that the terms must be subtracted
• It is easier to answer questions like finding equation of lines through (3,7) and (8, 2) because you don't have to find the y-intercept
• It can describe vertical lines (x=___) that have undefined slope
• It can be scaled by multiplying.  (by the way, dividing everything by C gives you an interesting form, x/dx-y/dy=1....)
• It is the form of choice for combining equations when systems of equations rolls around... my favorite topic in the algebra curriculum.
• It can easily be expanded into 3 (or more) dimensions, where y=mx+b has no easy expansion

To celebrate standard form, and praise some of its merits, I wrote a fight song for it, which is to the tune of the greatest college fight song out there, Michigan State.  The lyrics are posted below, as well as a link to a tune on Youtube so you can sing along.

A x + b Y equals C

is known as standard form by all

It always graphs a straight line

The only form that does them ALL

Other forms can't do straight up lines

'cause their slopes are undefined

We simply let x equals ___

 we'll be fine!

Chorus:

A's the rise and B's the run

As long as we subtract 'em!

Plug in a point to find the C

And make sure they are nice IN-TE-GERS!

Multi-pl'ing   by  de -nom'-na-tors

Makes fractions disappear! (poof!)

X's!  Y's!  Equals C!

Standard form's the one for me!

(Dance during musical interlude, then sing chorus again)