In her book Literacy Multiple Paths to Literacy, Joan Gipe describes literacy as multidimensional. I see literacy as having three unique axes, much like the x-, y-, and z-axes familiar to most math teachers. The literacy x-axis would be reading and writing. Both are communicating, but in different directions.
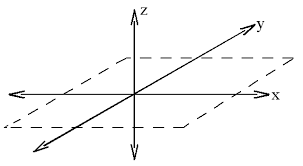
Reading is the input of information in written or typed form. Writing is in the opposite direction, as a person chooses to communicate by paper, pencil, or typed form. The literacy y-axis would be speaking, and listening. Again, both are different directions of the same method of oral communication. Finally, the z-axis would be viewing, and visually representing. This would be through pictures, demonstrations, gestures, graphs, and drawings.
My classroom is an algebra 1 and physics classroom. Before reading Gipe’s definition of literacy, I was certain that my classroom had very little literary content involved. We don’t do reading, I thought. However, Gipe described literacy as the ability to communicate, and not simply reading. Instantly I realized that there is a lot of literacy teaching going on in my classroom. Most of this is as the students in my algebra classrooms are learning to communicate using abstract ideas, and writing in a new language called algebra. I became aware that though I never teach finding subjects and verbs of sentences, I do teach them to break an expression down into individual terms. While I never teach my students how to sound out a word by emphasizing phonics, I do teach them to identify parts of terms, such as the sign, the coefficient, and the variable part.
In fact, I see all three dimensions of Gibe’s definition of literacy appearing in my classroom. In a very literal sense, students are reading the textbook, following examples. In a more general sense, students need to learn to read the language of algebra, by interpreting expressions, equations, formulas, and inequalities. Students need to write their answers using a new language, as well as communicate their thinking steps using the agreed upon conventional algebraic notation.
Students also operate among the speaking and listening dimension in class. I deliver much of the new information through lecture format, where students must listen and interpret. We often correct our assignments in class, sharing answers aloud where ‘pronunciation’ must often be addressed as students will say “x-two” instead of “x-squared” or “x to the second power.”
Many times in algebra, students are also learning new ways of illustrating relationships, by way of graphs. Most commonly this is via the Cartesian xy-plane and through graphs of lines and functions. We also use xy-tables to show relationships, and at times interpret other statistical graphs such as box-and-whisker-plots, pie charts, and scatterplots with line-of-best-fits. Students learn to make such graphs both on paper and on a computer, as well as how to interpret, and make extrapolation and interpolation predictions from such graphs.
In physics, we are doing much of the same, although at a deeper level. We spend much of our initial efforts focusing on the information that the units of an number can tell us, much like the use of various suffixes determines the type of word used. Our vocabulary has increased, and continues to grow as new quantities are precisely defined via formula. I teach specific writing skills as my students write lab reports, and I often need to correct their use of vocabulary words, such as the common effect/affect mistakes. Finally, graphs continue to be used, but primarily the line-of-best-fits becomes the tool of choice to show if and how two quantities are related.
My first reaction to taking a literacy course was that it was completely irrelevant to me as a high school math and science teacher. I initially had no motivation for the course, seeing it as just a hoop to jump through to earn my masters, and stay certified to teach. While I admittedly am not excited to take the course, I am happy to find that learning about teaching literacy will be much more applicable than I ever imagined.
You might recall from algebra class hearing about the Sieve of Eratosthenes? It works by going and counting by 2's and crossing every number, then counting by 3's and crossing out every number, and then 5's, and 7's, etc, until all that's left not crossed is the prime numbers.
