Vocabulary Model

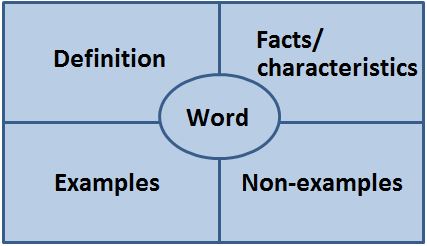
While reading Multiple Path's to Literacy, I was reminded of a technique I learned in a workshop once about teaching vocabulary -- especially math and science concepts.  Gipe called it the Frayer Model of vocabulary, which is summarized in the picture to the right. In this model, a definition, and examples are provided, as well as useful facts or characteristics. Also, several non-examples are listed, and I remember the presenter suggesting that students should list examples and non-examples -- and that you can provide equal praises for both.

For example, today we learned the vocabulary word "proportion" in algebra. The definition I provided was "an equation that compares two fractions"  Then I provided several examples such as 1/3 = 3/9 and x/5 = 24/40. One of the characteristics we mentioned was that true proportions can be cross-multiplied, which results in another true equation which doesn't contain fractions.  We also provided a non-example of 3/x=5 and also x/2+5 = 3/8.  

In physics, I have a similar model for teaching different quantities. I give a definition, a have a category called units, a category for examples, and a category for formulas containing that quantity. For example, "force" might have: 

   def: a push or pull on something

   units: Newtons, lbs, tons, ounces, (1 lb = 4.45 N) (16 ounces = 1 lb)

   examples: an apple weighs 1N.  Throwing a ball requires around 50 N.  

   formulas: Fnet = m*a,    Fgrav = m*g,  Ffric = mu*Fnormal ...

I like teaching vocabulary in a direct way -- and consistently.  I do that well in physics, but am not as organized in algebra. I'd like to consider giving each student a notebook to create a classroom dictionary -- but wonder if that's too childish for a high-school classroom?