Blue Elephants and Polynomial Equations

The other day in my precalculus class I used a series of jokes to make a point. We were studying polynomials, and how to solve polynomial equations such as:

Polynomial Equation:

The basic technique for solving a polynomial equation is to move everything to one side of the equals sign, and then search for the roots -- or x-intercepts of whatever is left.  This roots searching was something we had spent about a week practicing and refining, but hadn't yet discussed why one would bother looking for roots.  This example would lead to the equation 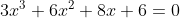 which has the graph: 

y=3x^3+6x^2+8x+6 has a root at x=-1.18
Image made in Geogebra

Since this equation has only one x-intercept, it has one solution, which is approximately -1.18.  (Yes, it also has two complex roots, but that's more than we need to discuss today).

One of the major reasons for finding roots is to solve these types of equations, but this root finding skill can also be useful in solving different types of equations. For instance, we learned how to solve "rational equations" which are polynomial equations with fractions involved: 

Rational Equation:

The basic strategy for this type of equation is to multiply by the denominators, which will eliminate the fractions, converting this ugly equation into a polynomial equation, which we can then find roots of.

We also learned how to solve "radical equations" using a similiar "convert and tackle" mentality:

Radical Equation:

The technique for these is to eliminate the radical by getting it alone one one side, and then squaring both sides. This will give you a polynomial equation which you can find the roots of.

This lesson reminded me of the blue elephant jokes I learned as a child, and shared with my students:

Teacher: How do you kill an elephant:

Student: I don't know

Teacher: With an elephant gun.  

Teacher: How do you kill a blue elephant?

Student: I don't know?

Teacher: With a blue elephant gun!

Teacher: How do you kill a pink elephant?

Student: With a pink elephant gun?

Teacher: No! You hold his trunk till he turns blue, and shoot him with a blue elephant gun.

Teacher: How do you kill a purple elephant?

Student: Hold his trunk till he...

Teacher: No! You first paint him pink, then hold his trunk till he turns blue and shoot him with a blue elephant gun. How do you kill a green elephant?

Student: Paint him ...?

Teacher: You fool! There's no such thing as a green elephant!

Students caught on pretty quickly to the absurdity of the jokes, but also saw the connection between killing blue elephants, and the equations we were slaying. One hour in particular enjoyed the metaphor and now calls all polynomial equations "blue elephants".