Unit Circle Trig Functions

I have been teaching my precalculus students how the trig functions can be defined by using the unit circle. Below is an animated .gif file that shows how each of the six trig functions can be defined using the unit circle:

The Six Trig Functions on the Unit CircleCreated with Geogebra
Downloadable image: (952 KB)
Downloadable Geogebra file: (5 KB)

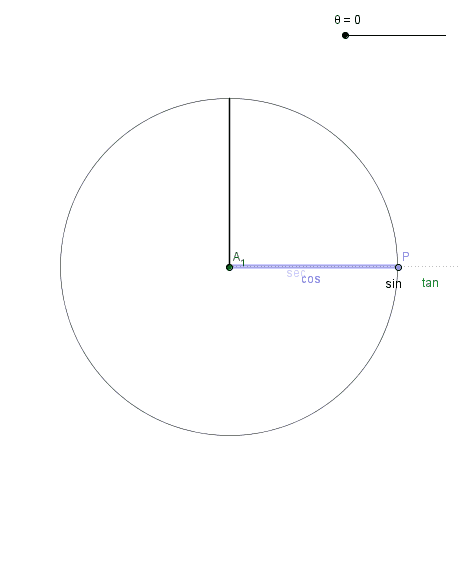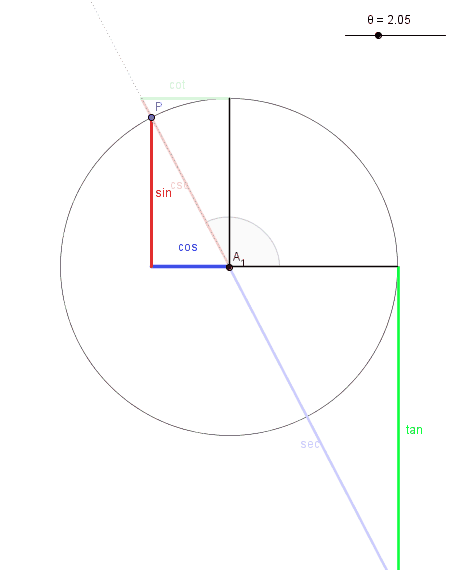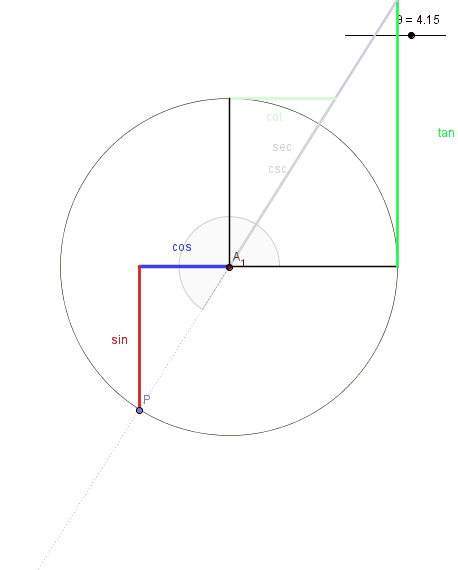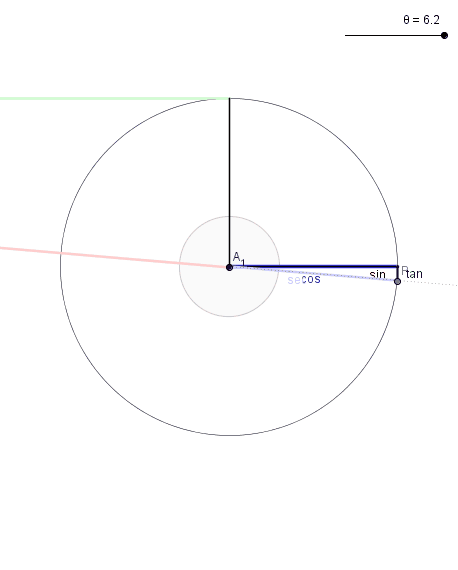
The angle in the animation ranges from 0 to 6.28 radians, which is 0 to 360 degrees. The circle is a unit circle, which means it has a radius of one. It is centered at (0,0) and the angles are measured in the typical counter-clockwise direction.  Each of the segments is then defined according to the following rules:

• Sine: The height of P, which is the where the angle intersects the unit circle. Sine ranges from -1 to 1, depending on whether P is below or above the x-axis.  
• Cosine: The x-coordinate of P, which again ranges from -1 to 1 depending on whether P is to the right or left of the y-axis.
• Tangent: if you extend the angle out until it means the line x=1, then the tangent will be the segment extending "tangent" to the circle from (1,0) to that intersection. If the angle is in quadrant II or IV, the intersection point is below the x-axis, and so tangent is negative. If the angle is in quadrant II or III, the angle wouldn't intersect the tangent line, unless you extend it backward. Notice it ranges through all values from -inf to +inf, and twice is undefined at 90 degrees and 270 degrees because at those points  the angle never intersects the line x=1 because they are parallel.
• Secant: if you extend the angle out until it meets the line x=1, then the secant will be the segment cutting through the circle, extending from (0,0) to that intersection. For quadrants II and III, the angle would have to be extended in the opposite direction, which is why secants have negative values there. Secant values are always greater than 1 (or less than -1) because they have to get through the unit circle and out to the line, and the smallest they can ever be is when they at angles 0 and 180 degrees. Like the tangent, secant is undefined for 90 and 270 degrees because the angle is parallel to the line x=1
• Cotangent: like the tangent, only everything is measured from the complement of 0, or 90 degrees. Extend the line outward until it meets the line tangent to the circle at 90 degrees, or y=1.  If this intersection is on the positive side of the x-axis, cotangent is positive, and negative if on the other side.  
• Cosecant: like the secant, only the length of the segment extending out to the line y=1. It can have negative values, when the angle is in quadrants III and IV because the angle would have to be extended backward instead

While it takes a day or two of practice for the students to get used to the definitions of the segments, I have found them to be especially useful.  I use these definitions to help estimate trig values, to determine their signs, to develop the idea of graphs of trig functions, and even to prove some identities.  The Pythagorean identities are especially nice to demonstrate here. I always remember 1+tan(x)^2 = sec(x)^2 because they are connected in their definitions, and adding the segment (0,0) to (0,1) creates a 90 degree triangle to which the Pythagorean theorem can be applied.