Adjacency Matrices

This post is a part of a series of guest-posts on the applications of matrix multiplication. These posts were written by my pre-calc students:

Adjacency Matrices 

By John Taylor 

Let’s say you have to go over to your friend Will’s house, but you have to get some things done first. How can you know how many routes you can take and gets to Will’s? Enter the adjacency matrix. This helpful matrix can tell you how many different routes you can take of the same number of moves to get to the same place. Now the first thing you should do when you are starting to get ready to make your matrix is to look at your map:

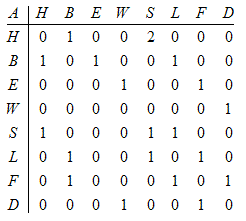
 Now figure out what these places are. The house is, well, your house. All the others, except W, are stores you need to go to: The sock shop (S), the book store (B), the library (L), the electronics store (E), the farmer’s market (F) and the drug store (D). The W is Will’s house. The next step is to write a matrix recording these relations. For each road from one place to another record a 1. If there is no connection put a zero. For a one-way street only write a 1 for the direction the arrow faces. If there are two options, say between home and the sock shop, enter a 2. This matrix will look like this.

Now we have this maps matrix. That was the hard part; now it’s quite simple. However many places you want to go to and raise the matrix to that power. (Note: This will give you all ways even if they repeat points. For the sake of this example you are very forgetful and often have to go back because you forgot many things at these stores.)

 Let’s go back to the trip to Will’s. You want to go to six places before you head over. Just raise the whole matrix to 6 and in the cell H,W you will see how many routes there are that reach Will’s in six moves. The resulting matrix will look like this:

Now look in the cell H,W and you will find out your answer. Even though most of the numbers are big, there are only 10 ways to get from your house to Will’s in 6 moves. This is the way adjacency matrices work. I hope this example has helped you understand these helpful matrices more fully.