This post is a part of a series of guest-posts on the applications of matrix multiplication. These posts were written by my pre-calc students:
Systems of Equations Matrix Project
by Jake Melton
Matrices have many different applications and can be helpful in many situations. One such situation is solving systems of equations. Solving systems of equations using matrices takes several steps, all of which will be explained in the following blog post. All of the steps will be shown as if you were using a TI-89 calculator (or Mr. Roer's edits show steps for a TI-82, -83, -84).
The following system of equations will be used as the example throughout the following post:
To begin the process we need to first write all of the equations in standard form (i.e. variables=number.) This will have to be done by hand. After we finish this process we get:
Once we have written this new system of equations there are two ways we could go. First, we could complete the system of equations by hand. This process would include writing two matrices A and B. A would be a coefficient matrix, that is a matrix written using the number by which the variable is multiplied; this matrix would be 4 by 4. The second matrix, B would be a 4 by 1 matrix written using the answers. Remember, if there is no variable as seen in the second equation where there is no x, you must write a 0. The system of equations is then summarized by the matrix multiplication:
To find the solutions, you can simply multiply the inverse of A by B and the resulting 4 by 1 matrix would be the answers, illustrated here.
*Note if the determinant of A equals zero the system has either no solution or many solutions.
However, to solve the system of equations we could follow another much more simple process using our calculators. Using a TI-89 (or TI-82, -83, or-84) first press “on” and scroll up to the data/matrix editor and press enter (or press 2nd Matrix). Select “new” then “matrix”. Next, enter the name you would like under “variable” and continue by pressing enter. The data should be empty, now simply enter your data into the table, making sure you enter a 4 by 5 matrix. This matrix is augmented [A|B] and will appear as follows.
As you can see, this matrix is simply both matrices shown on the previous page combined. Now, simply press “enter” then “home”. Next you will need to click the “catalog” button found in the middle of your calculator, then press “2” and scroll to “rref(” and hit enter. (or press 2nd Matrix, over to calc, and down to B: rref ) Now you will need to enter the name of your matrix using “alpha” and the name of your matrix. The rref you just entered stands for “reduced row echelon form of a” or as Mr. Roer calls it, “really ridiculously easy form” and it simplifies the equations for you to give you:
Each row is a simplified equation. The first row simply means that
1w +0x +0y +0z = 3.5 or, w = 3.5
So now that you have found this matrix you can conclude that:
w = 3.5
x = -4
y = -1.5
z = 2.5
These numbers shown above mean that w, x, y, and z are the only numbers that could be put into the original system of equations and make ALL of them true. And that is how you would go about finding the answer to a system of equations using matrices. Now you know how to solve these systems by hand or using your TI-89 calculator (or TI-82, -83, -84). Now use these steps to solve any difficult system of equations with ease. I hope you leave feeling enlightened and much smarter, or more confused, but hopefully the former.
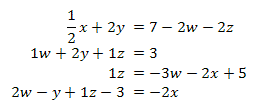





No comments:
Post a Comment